Przykłady zastosowania równania p·V = const w kompresorach, zbiornikach, siłownikach

1. Podstawy prawa Boyle’a-Mariotte’a

1.1. Definicja i warunki założeniowe

Prawo Boyle’a-Mariotte’a odnosi się do tzw. gazu doskonałego i stanowi, że jeśli proces zachodzi przy stałej temperaturze (proces izotermiczny) oraz ilość gazu się nie zmienia, to iloczyn ciśnienia p i objętości V pozostaje wielkością stałą. Matematycznie ujmuje się to zależnością:

p ⋅ V = const

lub w formie porównawczej:

p1 ⋅ V1 = p2 ⋅ V2

gdzie:

• p1, p2 – ciśnienia gazu w stanie początkowym i końcowym,

• V1, V2 – objętości gazu w stanie początkowym i końcowym.

Warunek utrzymania stałej temperatury w praktyce oznacza, że układ musi umożliwić wymianę ciepła z otoczeniem lub proces zachodzi na tyle wolno, że ciepło ma czas się wyrównać. W realnych warunkach sprężania w kompresorze czy gwałtownego rozprężania w siłowniku trudno o idealną izotermiczność, ale w wielu analizach wstępnych przyjmuje się to prawo jako przybliżenie – bądź jako odniesienie do bardziej skomplikowanych równań (np. przemiany politropowe, adiabatyczne).

2. Zastosowanie w układach przemysłowych i pneumatycznych

2.1. Rola pneumatyki w przemyśle

Pneumatyka – czyli technika wykorzystująca sprężone powietrze do zasilania maszyn, urządzeń i procesów – jest stosowana w niemal wszystkich gałęziach przemysłu: od lekkiej produkcji spożywczej, przez automotive, aż po ciężki przemysł maszynowy. Wszędzie tam fundamentalne znaczenie ma regulacja ciśnienia, zrozumienie zmian objętości i wynikających stąd sił oraz energii.

Prawo Boyle’a-Mariotte’a bywa kluczowe przy:

• obliczaniu pojemności zbiorników ciśnieniowych,

• analizie procesów sprężania w kompresorach,

• wyznaczaniu siły w siłownikach pneumatycznych przy zmiennym zakresie ciśnienia i skoku,

• dobieraniu parametrów układu (ciśnień, średnic przewodów, objętości buforowych) w celu utrzymania stabilnej pracy linii produkcyjnej.

3. Kompresory a prawo Boyle’a-Mariotte’a

3.1. Sprężanie izotermiczne – model teoretyczny

Weźmy kompresor tłokowy sprężający powietrze z ciśnienia atmosferycznego P atm do np. 8 barów (wartość manometryczna). W idealnie izotermicznym procesie:

P atm ⋅ V atm=P doc ⋅ V doc

gdzie:

• P doc – docelowe ciśnienie (np. 8 barów + 1 bar atmosferyczny = 9 barów absolutnych).

• V doc – objętość zmniejszona gazu po sprężeniu.

• V atm – objętość początkowa gazu (przed sprężeniem).

Zależność ta pozwala określić, o ile zmaleje objętość powietrza po osiągnięciu docelowego ciśnienia. W praktyce – zwłaszcza przy szybkiej kompresji – proces jest bliższy przemianie adiabatycznej (temperatura rośnie), a nie izotermicznej. Niemniej, na przykład w instalacjach z międzystopniowym chłodzeniem powietrza (kompresory wielostopniowe), dąży się do tego, by sprężanie było jak najbardziej zbliżone do izotermy, co minimalizuje pracę sprężania.

3.2. Wydatek kompresora a zmiany ciśnienia

Przy kompresorach decyduje też wydatek (ang. capacity) – czyli objętość powietrza w przeliczeniu na warunki odniesienia (najczęściej standard w kg/h lub m³/min w warunkach atmosferycznych). Dzięki równaniom zbliżonym do Boyle’a-Mariotte’a (uwzględniających też wpływ temperatury), można obliczyć, ile powietrza uzyskuje się w warunkach roboczych – np. przy 6 lub 10 barach manometrycznych.

Często przyjmuje się:

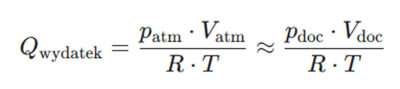
(w uproszczonej formie, z pominięciem współczynników gazu i niezmiennej temperatury). Dzięki temu można określić, ile realnie powietrza (w przeliczeniu na warunki atmosferyczne) daje kompresor przy danym ciśnieniu końcowym.

4. Zbiorniki powietrza (receivery) i rola prawa Boyle’a-Mariotte’a

4.1. Zadania zbiorników w instalacjach pneumatycznych

W typowym układzie przemysłowym istnieje co najmniej jeden zbiornik buforowy (tzw. receiver). Pełni on funkcje:

1. Magazynowania określonej objętości sprężonego powietrza,

2. Wyrównywania wahań ciśnienia przy nagłych poborach powietrza,

3. Stabilizacji pracy kompresora (mniej częste uruchamianie i zatrzymywanie).

4.2. Obliczanie minimalnej pojemności zbiornika

Kluczową kwestią jest dobór wielkości (objętości) zbiornika w zależności od wymaganego ciśnienia roboczego oraz chwilowego zużycia powietrza. Prawo Boyle’a-Mariotte’a pozwala oszacować, w jakim stopniu ciśnienie spadnie przy określonym poborze objętości powietrza w krótkim czasie.

Przykład:

• Instalacja pneumatyczna pracuje przy ciśnieniu 8 bar (absolutnie ~9 bar).

• Zbiornik o objętości Vzbior

• Zgodnie z prawem Boyle’a-Mariotte’a, jeśli w krótkim czasie pobierzemy objętość powietrza ΔV (w warunkach zbiornika), to nowe ciśnienie Pnowe będzie takie, że:

Zakładając, że proces jest izotermiczny (lub wolny na tyle, aby temperatura pozostała stała), możemy obliczyć, o ile spadnie ciśnienie po pobraniu ΔV sprężonego powietrza. To pozwala inżynierom określić, jak duży zbiornik jest potrzebny, żeby przy określonym jednorazowym poborze ciśnienie nie spadało np. poniżej 6 barów.

5. Siłowniki i prawo Boyle’a-Mariotte’a

5.1. Rola ciśnienia i objętości w generowaniu siły

W siłownikach pneumatycznych siła na tłoku wynika z prawa:

F = p ⋅ A

gdzie:

• p – ciśnienie robocze,

• A – Użyteczne pole powierzchni tłoka.

W trakcie ruchu tłoka objętość komory siłownika rośnie lub maleje. Przy założeniu wolnego ruchu i odprowadzania/podawania powietrza o stałym ciśnieniu, prawo Boyle’a-Mariotte’a może z grubsza opisywać relację między chwilowym ciśnieniem w komorze a jej objętością. Jednak w rzeczywistości siłowniki działają często dynamicznie, a powietrze jest stale dopływające bądź odprowadzane przez zawory.

5.2. Przykład – tłok zatrzymany w połowie skoku

Wyobraźmy sobie, że siłownik jest zasilany ciśnieniem 6 bar. W pewnym momencie tłok się blokuje, a zawory zasilania są zamknięte. Zakładając, że temperatura otoczenia i czas przestoju są na tyle długie, by proces można uznać za izotermiczny, to jeśli tłok zostanie przesunięty zewnętrzną siłą o małą wartość Δx– objętość komory maleje, a ciśnienie rośnie. W przybliżeniu można zastosować:

p1 ⋅ V1 = p2 ⋅ V2

Gdzie p1 to ciśnienie początkowe (np. 7 bar abs.), a V1 to objętość komory. Po zmniejszeniu objętości o ΔV uzyskamy nową wartość ciśnienia p2. Oczywiście w realnym układzie siłownik nie jest idealnie szczelny, a temperatura może rosnąć, jeśli sprężanie jest gwałtowne.

6. Praktyczne uwagi na temat procesów izotermicznych

6.1. Różnice między teorią a praktyką

• Sprężanie w kompresorach zachodzi szybko, zwykle przypomina bardziej przemianę adiabatyczną (bez wymiany ciepła).

• Rozprężanie w siłownikach także często jest dynamiczne i może prowadzić do spadku temperatury (efekt Joule’a-Thomsona, przemiana zbliżona do adiabatycznej).

• Układ chłodzenia kompresora (np. wymienniki ciepła, chłodnice międzystopniowe) pozwala przybliżyć się do warunków izotermicznych, co obniża pracę sprężania i ogranicza nagrzewanie gazu.

• Zbiorniki sprężonego powietrza – w warunkach ustalonych (długotrwałe przechowywanie powietrza, niewielkie pobory) można przyjąć, że procesy zmian ciśnienia są bliskie izotermicznym.

6.2. Politropa – rozszerzenie konceptu Boyle’a-Mariotte’a

Inżynierowie często stosują pojęcie przemiany politropowej:

P ⋅ Vn = const

gdzie n to wykładnik przemiany (dla izotermicznego n=1, adiabatycznego ~1,4 dla powietrza). To umożliwia bardziej precyzyjne modelowanie realnych zjawisk. Prawo Boyle’a-Mariotte’a jest zatem przypadkiem szczególnym (izotermicznym, n=1).

7. Przykładowe zastosowania równania p ⋅ V = const

1. Projekt zbiornika buforowego:

• Założenie: Chcemy, aby przy poborze ΔV (powietrze liczone w objętości zbiornika, ciśnienie nominalne) ciśnienie nie spadło poniżej Δp.

• Obliczenia: Korzystając z  Ppoczątkowe ⋅ Vzbior= Pnowe⋅ (Vzbior−ΔV) znajdujemy minimalną wartość  Vzbior, aby Pnowe≥ Pminimalne.

2. Określenie ciśnienia końcowego:

• Założenie: Kompresor tłokowy pracuje wolno i ma chłodzenie, chcemy przyjąć izotermę.

• Obliczenia:   p1 ⋅ V1 = p2 ⋅ V2 . Daje to wstępną aproksymację temperatury końcowej i ciśnienia (uwzględniając, że w rzeczywistości  T rośnie, więc ciśnienie rzeczywiste może być wyższe).

3. Symulacja w siłowniku pneumatycznym:

• Założenie: W pewnych momentach tłok jest unieruchomiony i powietrze jest odcięte.

• Obliczenia: W niewielkiej skali ruchu (Δx małe) można oszacować, jak rośnie / maleje ciśnienie w komorze według   p1 ⋅ V1 = p2 ⋅ V2 , co przekłada się na siłę tłoka.

8. Wnioski i podsumowanie

Prawo Boyle’a-Mariotte’a stanowi podstawę analizy izotermicznego zachowania gazu w układach pneumatycznych. W kompresorach realny proces różni się od izotermy, lecz równanie P ⋅ V = const jest punktem wyjścia do bardziej zaawansowanych modeli (np. politropy). W zbiornikach to prawo pomaga określić, jak zmieni się ciśnienie przy poborze określonej objętości powietrza, dzięki czemu inżynierowie dobierają optymalną pojemność bufora. W siłownikach rozważania na poziomie izotermicznym przydają się w spoczynkowej fazie ruchu lub przy małej dynamice, choć w szybkim ruchu przeważa zwykle efekt adiabatyczny. W praktyce nie można zapominać, że przemiany w pneumatyce często są dynamiczne – dlatego ciepło nie zawsze ma czas się wyrównać, a efektywne procesy sprężania czy rozprężania wymagają wprowadzenia chłodzenia (kompresory międzystopniowe) lub dedykowanych rozwiązań (np. zaworów szybkiego spustu). Współczesne układy przemysłowe wykorzystujące pneumatyczne systemy – od linii montażowych, przez roboty manipulacyjne, aż po instalacje do testowania szczelności – korzystają w dużej mierze z idei stojącej za prawem Boyle’a-Mariotte’a. Rozumienie tej przemiany izotermicznej (nawet jeśli w rzeczywistości idealizuje się proces, bo przy czerpaniu powierza (a więc mieszaniny gazów) z otoczenia – to wytwarzane sprężone powietrze zawiera także znaczne ilości wody w fazie gazowej lub jako aerozol) - znacznie ułatwia projektowanie efektywnych instalacji, pozwala na kontrolę i redukcję kosztów energii związanych z kompresją powietrza, a także zapewnia niezawodną pracę urządzeń w różnych warunkach eksploatacyjnych.

Autor:
Krzysztof Kornacki
Product Manager
Pneumat.

Autor:
Krzysztof Kornacki
Product Manager
Pneumat.